Some technical discussions on behaviour of decision tree splitting
18 Aug 2021 [decision-tree How does a regression decision tree choose on which feature to split?
This is like Data Science 101, so I will not go through the details. You can read [1] to refresh the memory. Here is the rough idea:
- Do the following steps for every feature $\mathbf{x}_1,\cdots,\mathbf{x}_p$
- Sort $(x_i, y)$ in non-descending order of $x_i$. Call the sorted pair $(x_i’, y’)$. Note that for different $x_i$’s we will get different $y_i’$.
- Divide $\mathbf{y}’$ (i.e. the sorted $\mathbf{y}$) into a left part $L = \{y_i’ \le y_1’\}$ and a right part $R = \{y_i > y_1’\}$, and compute something called impurity. For regression tree, a commonly used impurity measure is $SS(L) + SS(R)$. Here, $SS$ is the sum of squared error, defined as $SS(x_1,\cdots,x_n) = \sum_{i=1}^n (x_i - \bar{x}_n)^2$, where $\bar{x}_n$ is the sample average.
- Repeat the previous step, but change $y_1’$ to $y_2’, y_3’, \cdots, y_n’$.
- We have examined $n$ different partitions. Keep the one that gives the smallest impurity $SS(L) + SS(R)$
- Now we have the smallest impurity $SS(L) + SS(R)$ for each feature. Choose the feature with the smallest overall impurity.
The question I was interested in was this:
Question 0: Is there any smarter way to find the best feature $\mathbf{x}$, without going through all the features? If not, is there any smarter way to understand the whole process at least?
If you examine the algorithm, obviously the magic happens when we create partition $L$ and $R$ on the sorted vector $\mathbf{y}’$. To get to the essence of the problem, let’s ignore $\mathbf{x}_i$ for now, and think about the following problem:
Question 1: Given a vector $\mathbf{y}$, and re-order it (or equivalently, permute it) to get another vector $\mathbf{y}’ := \pi(\mathbf{y})$. We then partition the re-ordered vector $\mathbf{y}’$ into a left part $L$ and a right part $R$. If we want to minimize $SS(L) + SS(R)$, how should we re-order $\mathbf{y}$ (i.e. what is the optimal $\pi^*(\cdot)$)? How should we partition it after that?
Note that we are only allowed to cut the array in half from the middle. For example, if we have $\mathbf{y} = \{1, 2, 3, 4\}$, we can’t say that $L = \{1, 3\}$ because there is a $2$ between them.
For simplicity, let’s define order function $o(\mathbf{x})$. This is the same as order() in R. For example, $o([5,2,7]) = [2,1,3]$. If we can answer Question 1, then we can think of Question 0 in this way:
There is a permutation $\pi^*$ such that if you partition $\pi^*(\mathbf{y})$ into a left part and a right part, you can minimize $SS(L) + SS(R)$. To find the best feature, we just need to find the feature $\mathbf{x}^*$ such that $|o(\mathbf{x}^*) - o(\pi(\mathbf{y}))|$ is as small as possible.
Or at least that’s what I thought…
How to find the best partition if $\mathbf{y}$ is sorted already? (Answer: Brute force)
I started with a seemingly easier question: Assume $\mathbf{y}$ is already sorted. Is there any analytical way to find the optimal split point (Note that we can always just scan through all $n$ possibilities)? Formally,
Question 2: Assume $\mathbf{y} = (y_1, y_2, \cdots, y_n)$ is sorted in ascending order. We want to divide $\mathbf{y}$ into a left part $L = \{y \le y_s\}$ and a right part $R = \{y > y_s\}$. How to find a $y_s$ that minimizes $SS(L) + SS(R)$?
At first, I thought sample average and sample median were two promising candidates. Intuitively (at least to me), if we want to make $SS(L) + SS(R)$ small, then the points within each group should be close to each other. As a result, we probably shouldn’t put sample maximum and minimum in the same group.
And indeed, for many samples, the best splitting point $y_s$ is the median or the mean. For example, if $\mathbf{y} = \{1, 2, 3\}$, then we should split it into $L=\{1,2\}$ and $R =\{3\}$. Another good example is $\mathbf{y} = \{1, 2, 3, 4\}$. Here, $y_s = 2$, which is a median.
But it’s also easy to find counterexamples. Consider $\mathbf{y} = \{1, 3, 6, 8, 10\}$. It turns out that the best split point is $y_s = 3$. This is neither mean nor median. In fact, sometimes it’s not even close to the “center” of the sample. In the following example, the best split point is the black vertical line. It is quite far from the sample median (in blue) and the sample average (in red).
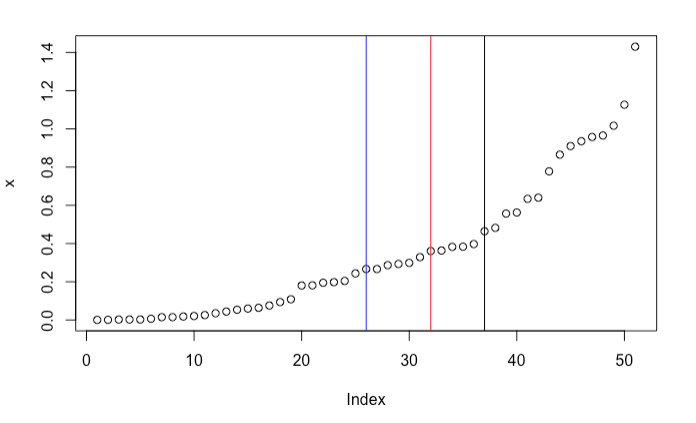
It seems that there is no analytical solution. You might not be surpried. After all, this is a special case of the more difficult $k$-means clustering problem. Here, we are dealing with a 1-dimensional 2-means clustering problem. For 1-dimensional $k$-means clustering, you can use dynamic programming to find a global optimizer. See referenece [2] for details.
In conclusion, even when $\mathbf{y}$ is sorted, there is no analytical way to find the best split $y_s$. We can always linearly scan through it. So that’s not too bad.
Can I find the best partition on unsorted $\mathbf{y}$? (Answer: In most cases, no)
In general, $\mathbf{y}$ will not be sorted. In such cases, we can still scan the whole thing, and find the best partition for that specific ordering. But how do we know if it is the best one among all possible partitions? See the following example:
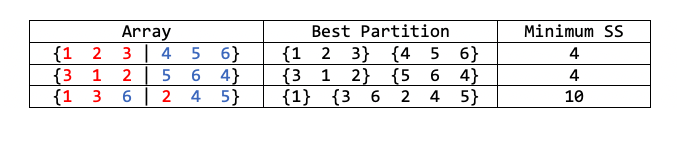
If we are given the third array, we will find that $\{1\}, \{3,6,2,4,5\}$ is the best partition. But it is not the best one globally.
In order to tackle the situation, let’s notice a few things. Let $\mathbf{y}$ be in any order, and $L, R$ be any of its $n$ left/right partitions. We can categorize $(L, R)$ into 2 types:
- Type I: $\max(L) \le \min(R)$. For example, $L = \{3,2,1\}, R = \{4,6,5\}$. In such case, we write $L \lhd R$.
- Type II: $\max(L) > \min(R)$. For example, $L = \{1,2,4\}, R = \{3,6,5\}$.
Adopting this view, we immediately conclude the following:
- If $\mathbf{y}$ is sorted, then every partition $(L, R)$ satisfies that $L \lhd R$.
- If $\mathbf{y}$ is not sorted, then some of its partitions might still satisfies that $L \lhd R$.
Let’s go back to this example:

The first array is already sorted. No matter how you split it in half, you always end up with $L \lhd R$. The second array is not sorted, but $L = \{3, 1, 2\}, R = \{5, 6, 4\}$ still satisfies $L \lhd R$. However, if we split the second array into $\{3\},\{1,2,5,6,4\}$, then the condition is not satisfied, since $3 > 1$.
Here comes the main result.
Let $\mathbf{y}$ be in any order, and $(L, P)$ be any partition. Assume $\mean(L) < \mean(R)$. As long as $L \lhd R$ does not hold, we can switch $\max(L)$ and $\min(R)$ to make $SS(L) + SS(R)$ smaller. In other words, $L \lhd R$ is a necessary (but not sufficient) condition to minimize $SS(L) + SS(R)$.
The proof involves some tedious-but-not-difficult algebra. Click here to see the details.
Without losing generality, we assume the left partition $L = \{x_1,x_2,x_3,x_5\}$, and $R = \{x_4,x_6,x_7\}$. Denote the average of $L$ as $\bar{x}_L$ and the average of $R$ as $\bar{x}_R$. We assume that both $L$ and $R$ are sorted in ascending order, $\bar{x}_L \le \bar{x}_R$, and that $x_5 \ge x_4$. Before we swap $x_4$ and $x_5$, the $SS$ is $$SS = (x_1 - \bar{x}_L)^2 + \cdots + + (x_5 - \bar{x}_L)^2 + \cdots + (x_4 - \bar{x}_R)^2 + \cdots + (x_7 - \bar{x}_R)^2$$ After we swap them, then SS becomes $$SS' = (x_1 - \bar{x}_L')^2 + \cdots (x_4 - \bar{x}_L')^2 + \cdots + (x_5 - \bar{x}_R')^2 + \cdots + (x_7 - \bar{x}_R')^2$$ where $\bar{x}_L' = \frac{1}{4} (x_1 + x_2 + x_3 + x_4)$, and $\bar{x}_R'$ is defined similarly. Using the identity $\sum (x_i - \bar{x}_n)^2 = \sum x_i^2 - n \bar{x}_n^2$, and subtract $SS'$ from $SS$, we have $$SS - SS' = (x_5^2 - x_4^2 - 4 \bar{x}_L^2 + 4 \bar{x}_L'^2) + (x_4^2 - x_5^2 - 3 \bar{x}_R^2 + 3 \bar{x}_R'^2)$$ After some algebra, we end up with $$SS - SS' = (x_5 - x_4)(\bar{x}_R - \bar{x}_L + \bar{x}_R' - \bar{x}_L')$$ By assumption, we have $x_5 - x_4 \ge 0$ and $\bar{x}_R - \bar{x}_L \ge 0$. The term $\bar{x}_R' - \bar{x}_L'$ is also greater than zero for obvious reason. In other words, we just made $SS$ smaller by swapping.
The implication, however, is this: If you want to find the best $(L, R)$ globally, you should always start with a sorted $\mathbf{y}$. Because only a sorted $\mathbf{y}$ can guarantee that $L \lhd R$, which is a necessary (but not sufficient) condition for minimizing $SS$.
To be continued in the next post.
References