Decision tree and variables having lots of levels

Once a friend of mine asked me what to do with his dataset. He was trying to fit a tree model to the data at hand, but one of the categorical has too many levels. As a result, he felt it was necessary to do “pre-processing” on that variable. This is a common belief among data scientists: categorical variables having too many levels can cause trouble for tree-based models. Documentation of scikit-learn even has a dedicated article on this topic, see [1].

But how many level is too many? Why does large cardinality cause trouble? Does large cardinality always cause trouble? These questions caught my interest and hence we have this blog post now.

It’s not about how many levels $X$ have, but about…?

Data scientists tend to say things like “Oh, my variable $X_2$ has too many levels, so…”. But in reality, it’s not about how many levels $X_2$ have, but about how many partitions it can induce on $Y$. Recall that when a tree makes a split, it will

1. Scan through all the variables $X_1, X_2, \cdots, X_p$
2. For each variable, scan through all the possible partitions on $y_i$’s by which this variable can create. Specifically,
   1. If $X_j$ is numerical and has values $x_{j1},x_{j2},\cdots,x_{jm}$ present in the data, we look at all sets ${y_i \mid x_i \le x_{ik}}$
   2. If $X_j$ is categorical and has levels $a, b, c$ present in the data, then we look at all sets ${y_i \mid x_i \in \text{some subset of } \{a,b,c\}}$
3. Find the best variable and its best split

So, in fact, it’s not that the cardinality of $X_i$ that matters. Rather, it’s the cardinality of the set of partitions it can induce matters. Specifically, if $X_j$ is a categorical variable with $q$ levels, then it creates $2^q - 1$ partitions. On the other hand, if $X_j$ is a numeric with $q$ distinct values, then it creates only $q$ partitions. In fact, that’s why randomForest package in R cannot handle categorical variables with more than 32 categories. Because a categorical variable with 32 cateogires induces 2,147,483,647 partitions on $y_i$’s. See [2].

Sure. But still, if $X$ has many levels, it induces more partitions on $y_i$’s, so it’s always a problem…?

The answer is “yes” most of the time in practice. However, in some sense, the reason lies not in $X$ but other independent variables.

Let us consider a simple example. We simulate $n$ data points from $Y = 3X_1 + \epsilon$ where $\epsilon$ is some noise. Now, we add a categorical variable $X_2$ with many levels. Given the data, will the tree split using $X_1$ or $X_2$?

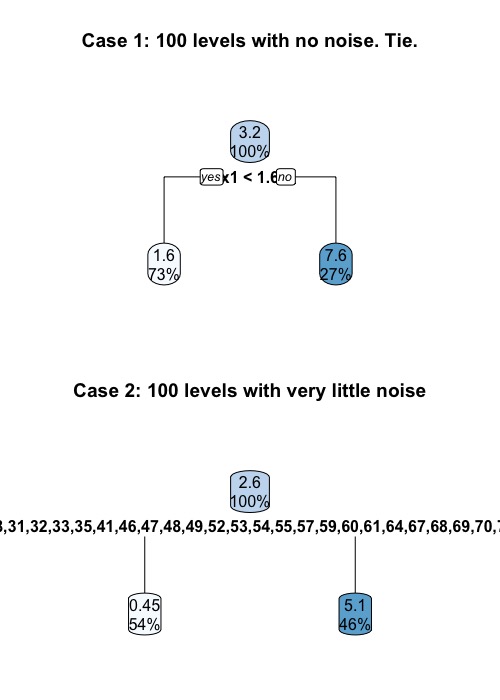
It is easier to consider two extreme cases. First, let us assume that there is no noise term. That is, $Y = 3X_1$ exactly. In this case, the tree will split using $X_1$ all the time. Even if we have $n$ levels in $X_2$, we will get a tie. On the other hand, if we have $n$ levels in $X_2$ and we have even a little bit noise, the tree always favor $X_2$. This is because any partition induced by $X_1$ can be induced by $X_2$, but not the other way around.

> set.seed(45)
> par(mfrow = c(2, 1))
> x1 <- rnorm(mean = 1, n=100)
> y <- 3*x1
> x2 <- as.factor(seq(1, 100))
> df <- data.frame(x1, x2 = sample(rep_len(x2, length.out = 100)), y)
> 
> fitted_cart <- rpart(y ~ x1 + x2, data=df, method = "anova",
+                      control = rpart.control(minsplit = 2, maxdepth = 1))
> rpart.plot(fitted_cart, main = "Case 1: 100 levels with no noise. Tie.")
> print(fitted_cart$splits)
   count ncat   improve    index adj
x1   100   -1 0.5994785 1.552605   0
x2   100  100 0.5994785 1.000000   0
> 
> 
> # Number of level equals to sample size, with a little bit of noise
> x1 <- rnorm(mean = 1, n=100)
> y <- 3*x1 + rnorm(n = 100, sd = 0.5)
> x2 <- as.factor(seq(1, 100))
> df <- data.frame(x2 = sample(rep_len(x2, length.out = 100)), x1, y)
> 
> fitted_cart <- rpart(y ~ x2 + x1, data=df, method = "anova",
+                      control = rpart.control(minsplit = 2, maxdepth = 1))
> rpart.plot(fitted_cart, main = "Case 2: 100 levels with very little noise")
> print(fitted_cart$splits)
   count ncat   improve     index       adj
x2   100  100 0.6414503 1.0000000 0.0000000
x1   100   -1 0.6371685 0.9917295 0.0000000
x1     0   -1 0.9800000 0.9079153 0.9565217

However, as expected, it is more difficult to draw conclusion on any less extreme cases (e.g. We have 1000 data points, and $X_2$ has 20 levels). “How many level is too many?” is a difficult question to answer. However, we can do a simple simulation to get some general idea:

set.seed(42)

library(rpart)

result <- c()
std_list <- seq(0.1, 4, 0.05)
for (std in std_list) {
  fv <- 0
  
  for (cnt in seq(1, 200)) {  # For each std, simulation 200 times
    x1 <- rnorm(mean = 1, n=100)
    y <- 3*x1 + rnorm(n = 100, sd = std)
    x2 <- as.factor(seq(1, 90))
    df <- data.frame(x2 = sample(rep_len(x2, length.out = 100)), x1, y)
    
    fitted_cart <- rpart(y ~ x2 + x1, data=df, method = "anova",
                 control = rpart.control(minsplit = 2, maxdepth = 1))
    
    if (data.frame(rpart.rules(fitted_cart))$Var.3[1] == "x2") {
      fv <- fv + 1
    }
  }
  
  result <- c(result, fv/200)
}

plot(std_list, result,
     xlab = "Standard deviation of noise",
     ylab = "Prob. of choosing the categorical variable X2",
     main = "How often does the tree choose the categorical variable X2?")

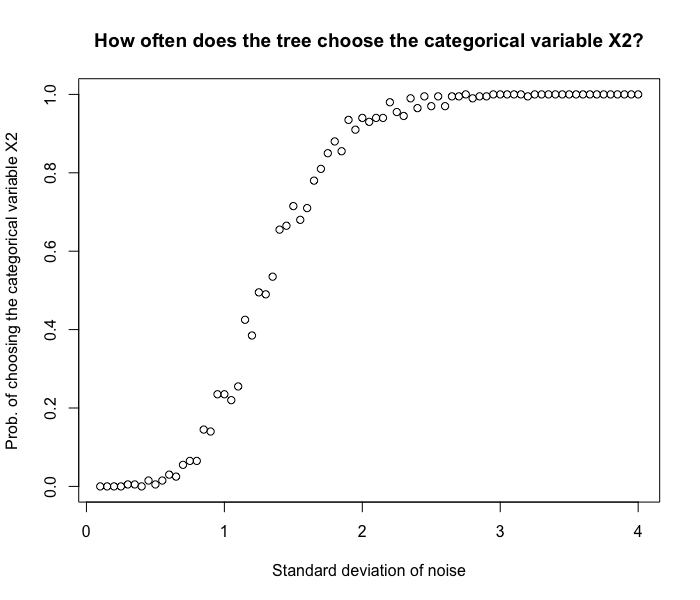
In this simulation, we generate 100 data points. from $Y = 3X_1 + \epsilon$ with different noise levels. We then see how likely the tree will make a split using $X_2$, the unrelated categorical variable with 90 levels. From the graph, we see that

1. Even though we have a cat variable with lots of levels, when the noise level is small, the tree still chooses the right variable $X_1$ to make a split.
2. When the noise level increases, it becomes more and more difficult to make a good split using $X_1$. Since $X_2$ has many levels and creates more partitions on $y_i$’s, the tree tends to use $X_2$.

In order to better understand the role of “noise level/variance level”, we should realize that decision tree has a very interesting property: Even though the whole tree forces all variables to interact with each other, it essentially does a sequence of univariate analysis at each node.

For example, at any given node, it might be the case that two variables gender and year_of_education combined can explain $y_i$’s pretty well, thus reducing the variance. But when we look at them individually, none of them is highly correlated with $y_i$’s. Under such situation, a third unrelated categorical variable with lots of level might be favored. This type of situation is probably very common in practice. So it is very understandable that people think categorical variables with many levels tend to cause problems.

Sample size also matters

It can also be demonstrated that if we keep the number of levels of $X_2$ fixed but increase the sample size, the decision tree becomes less likely to be tricked by $X_2$. This should not be surprising.

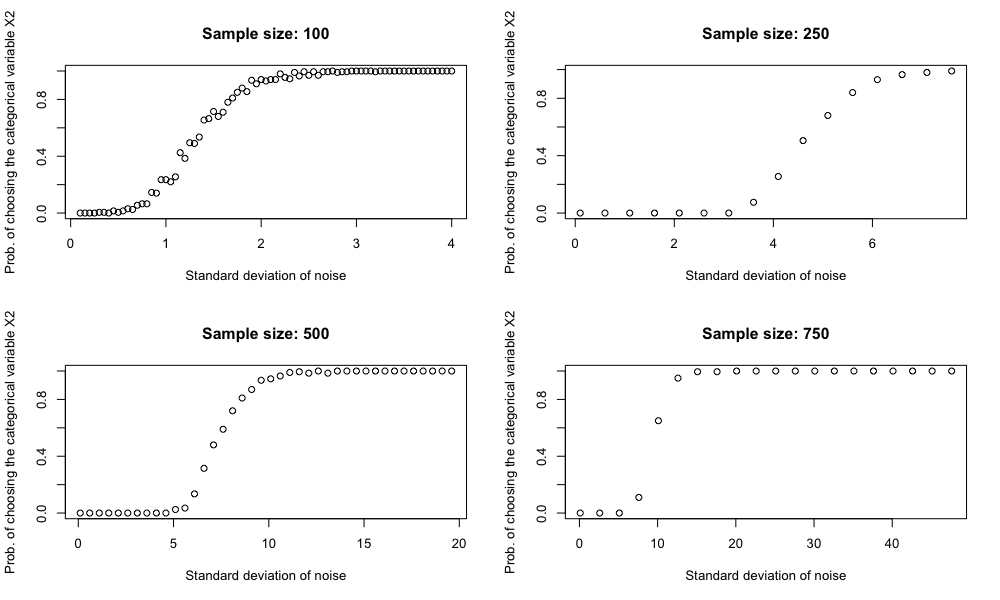
In practice, even though we have a large data set, we might still run into trouble. Because as the tree grows deeper, the sample size within each partition becomes smallers and smaller. For example, if we start with 100,000 data points and we grow our tree 3 levels deep perfectly balanced, we end up with only 12,500 data points.

References:

1. https://scikit-learn.org/stable/auto_examples/inspection/plot_permutation_importance.html#sphx-glr-auto-examples-inspection-plot-permutation-importance-py
2. https://stats.stackexchange.com/questions/49243/rs-randomforest-can-not-handle-more-than-32-levels-what-is-workaround